洛谷1073 最优贸易

题意

给出一个有向图，需要从 $1$ 走到 $N$ ，可以在一个城市买水晶球并在另一个城市卖掉，也可以不买，问最多能赚多少钱。

其中 点数$n\le 100000$ ，边数$m\le 500000$ 。

题解

分层图最短路。对于原图，买卖操作各建一层图，边权为在起点买卖水晶球的花费（买为负卖为正）。给原图、买、卖分别编号为 $1,2,3$ 。

已知 $x$ 点买卖水晶球的花费为 $s[x]$ ，对于每条边 $(x,y)$ 具体建图如下：

1. 每一层同层上不涉及买卖操作，所以所有边权都为 $0$ 。
2. 第 $1$ 层连向第 $2$ 层的边权为 $-s[x]$ （买入水晶球）
3. 第 $2$ 层连向第 $3$ 层的边权为 $s[x]$ （卖出水晶球）

还需要建立一个终点，因为买了肯定要卖不然血亏，所以连向终点有两种情况：

1. 第 $1$ 层的 $N$ 连过去
2. 第 $3$ 层的 $N$ 连过去

这样建两条边就行了。

对于样例得到的图如下：（感谢 @fy1234567ok）

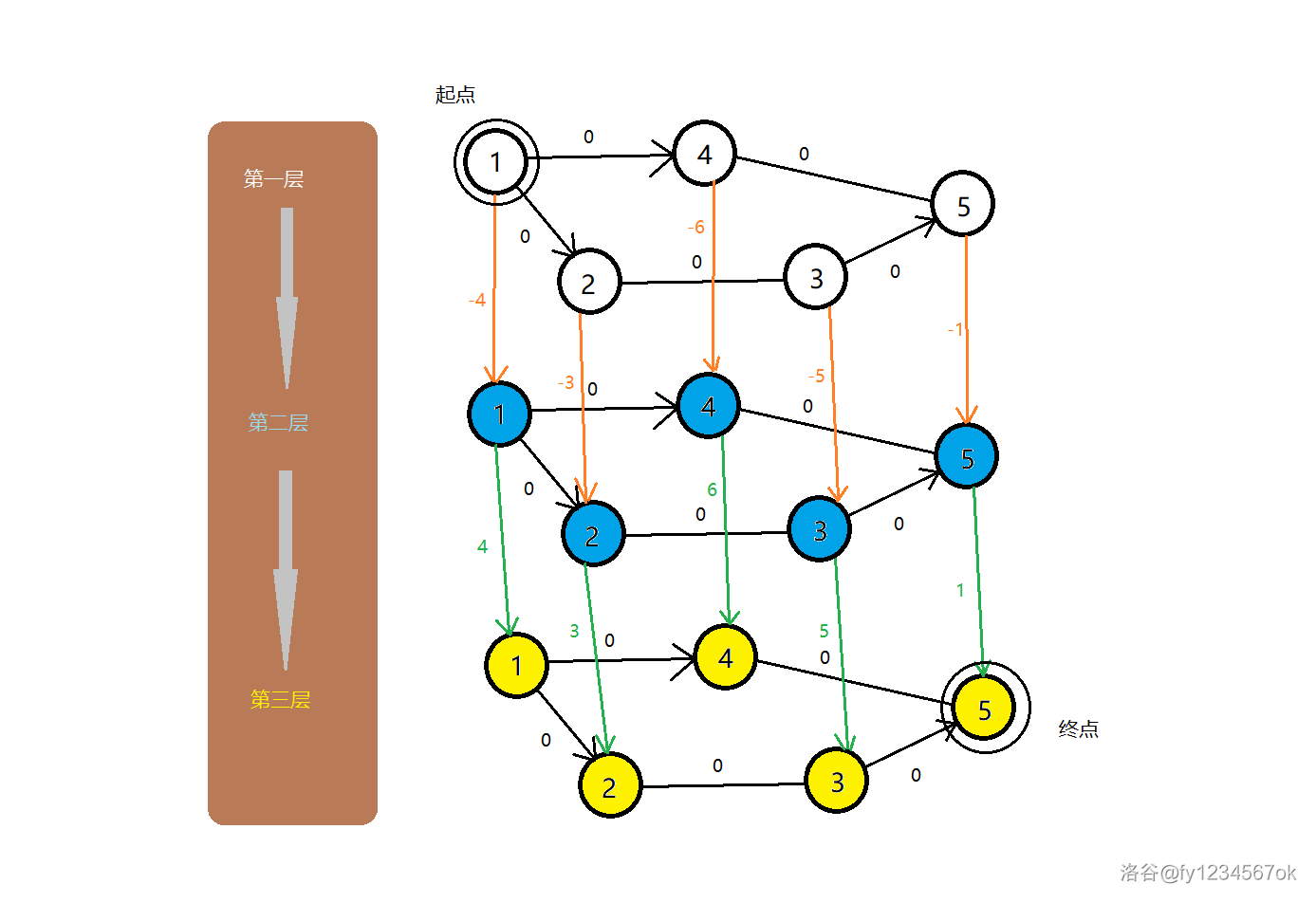
然后从第 $1$ 层的节点 $1$ 开始跑最短路就行了。因为有负权边，所以用 $spfa$ 。

#include<bits/stdc++.h>
#define fin n*3+1

using namespace std;

inline int read()
{
    char ch=getchar();
    int f=1,x=0;
    while (ch<'0' || ch>'9')
    {
        if (ch=='-') f=-1;
        ch=getchar();
    }
    while (ch>='0' && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return f*x;
}

struct Edge {
    int next,to,w;
} edge[3000005];
int cnt,head[300005],n,m,a,b,c,s[100005],dis[300005];
bool in[300005];

inline void add(int u,int v,int w)
{
    edge[++cnt].to=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt;
}

inline int get_id(int x,int cnt) { return n*(cnt-1)+x; }

inline void adde(int u,int v)
{
    add(u,v,0);
    add(get_id(u,2),get_id(v,2),0);
    add(get_id(u,3),get_id(v,3),0);
    add(u,get_id(v,2),-s[u]);
    add(get_id(u,2),get_id(v,3),s[u]);
}

inline int spfa()
{
    memset(in,0,sizeof(in));
    memset(dis,-0x3f,sizeof(dis));
    dis[1]=0;
    queue <int> q;
    q.push(1);
    in[1]=1;
    while (!q.empty())
    {
        int x=q.front(); q.pop();
        in[x]=0;
        for (int i=head[x];i;i=edge[i].next)
        {
            int y=edge[i].to,w=edge[i].w;
            if (dis[x]+w>dis[y])
            {
                dis[y]=dis[x]+w;
                if (in[y]) continue;
                in[y]=1;
                q.push(y);
            }
        }
    }
    return dis[fin];
}

int main()
{
    n=read(); m=read();
    for (int i=1;i<=n;i++) s[i]=read();
    for (int i=1;i<=m;i++)
    {
        a=read(); b=read(); c=read();
        adde(a,b);
        if (c==2) adde(b,a);
    }
    add(n,fin,0);
    add(get_id(n,3),fin,0);
    printf("%d",spfa());
    return 0;
}