这是整理的讲课材料,有些知识点仅有思路。
基础常识
进制转化
- 十转其他:整数部分除2取余,逆序排列;小数部分乘2取整,顺序排列。
- 其他转十
- 其他转其他:用十进制做跳板、二转八和十六进制的特殊情况。
机器码
- 带符号数:最高位表示符号,0为正,1为负;其他表示数值。
- 原码:符号位为0或1(正或负),数值不变。注意+0和-0不同。
- 反码:正数与原码相同;负数符号位不变,其他按位取反。
- 补码:正数与原码相同;负数符号位不变,其他按位取反后+1。
- 补码的意义:$A-B=A+(-B)$,在有模数的情况下 $A-B\equiv A+(M-B) \pmod M$,二进制下即需要$+1$
- 机器使用补码,$[10000000]$ 表示 $-128=(-1)+(-127)$,只有 $[00000000]$ 表示 $0$
- 程序中的应用,如
&,|,~(区分&&,||,!)
for (int i=100;i;i--)
for (int i=100;~i;i--)浮点数
$$N = 2^{E} \times S$$
$E$ 是阶码,为整数,表示小数点移动的位数(正数向右,负数向左)。
$S$ 是尾数,为二进制小数。
如 $101.011 = 2^{3} \times 0.101011 \ , \ 0.0101011 = 2^{-1} \times 0.101011$
ASCII码
7位二进制数,0~127共128个字符。
算法
排列组合
卡特兰数
$$\frac{C_{2n}^n}{n+1}$$
- 按 $1,2,\cdots,n$ 的顺序进栈,对应的出栈序列总数。
- $n$ 个点可以构成的二叉树种类数。
- (初赛无关)在$n\times n$个方格形成的地图中,只能向下向右走,不能越过对角线,从左上到右下格子的路线总数。
- (2016全国卷III数学 12)定义“规范01数列”$\{a_n\}$ 如下:$\{a_n\}$ 共有 $2m$ 项,其中 $m$ 项为 $0$,$m$ 项为 $1$,且对任意的 $k\le 2m$,$a_1,a_2,\cdots ,a_k$ 中 $0$ 的个数不少于 $1$ 的个数。若 $m=4$,则不同的“规范01数列共有”多少个?
树
二叉树
- 先序遍历:根左右;中序遍历:左根右;后序遍历:左右根
- 第 $i$ 层有最多 $2^{i-1}$ 个节点。
- 深度为 $k$ 的二叉树最多有 $2^k-1$ 个节点,最少有 $k$ 个。
- 满二叉树:深度为 $k$ 就有 $2^k-1$ 个节点。
- 完全二叉树:除了最下层外的其他层都满,满二叉树也是完全二叉树。
哈夫曼树
哈夫曼树是最优二叉树,即每个点的权值 $\times$ 它到根节点的路径和最小。
哈夫曼树的构建方法是先将每个点单独构建成一颗只有自己的树,然后每次选取路径和最小的两棵树合并到一起,所有树合并完即构建成功。
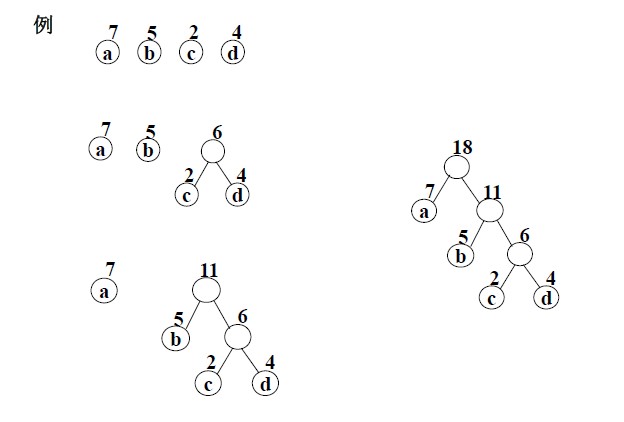
例题:设某哈夫曼树中有199个结点,则该哈夫曼树中有()个叶子结点。
- A、 99
- B、 100
- C、 101
- D、 102
答案:B
解析:把 $ n $ 个节点构建成哈夫曼树,相当于把 $ n $ 个只有根节点的子树合并成一个树,其中将任意两个子树合并成一个棵树需要增加一个节点,则一共需要增加 $ n-1 $ 个节点,才能使其变成一棵哈夫曼树,即这棵哈夫曼树一种有 $ 2n-1 $ 个树。$ 2 \times n - 1 = 199 $ ,解得:$n = 100$
二叉搜索树
若左子树不为空,则左子树所有节点均小于根节点;若右子树不为空,则右子树所有节点均大于根节点。
堆
- 性质:根节点大于其他节点。(左右子树无要求)
- 插入:(大根堆)先将其接在最后,然后判断它与父节点大小关系,若大于父节点则交换,并重复这个步骤,直到小于父节点时停止。
- 删除根节点:将最后一个元素替换根节点,并进行与插入操作类似,不过依次向下的修复。
排序
排序的稳定性
稳定的排序:若排序前数 $a_i=a_j$ 且 $a_i$ 在 $a_j$ 之前,排序后 $a_i$ 仍然在 $a_j$ 之前。
- 稳定排序:插入排序、桶排序、基数排序
- 不稳定排序:快速排序、堆排序、希尔排序、归并排序、选择排序、冒泡排序
冒泡排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 |
比较相邻的元素,如果前比后大就交换。
需要注意最好时间复杂度是 $O(n)$ ,可以在代码中加上判断是否有交换。
选择排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
从未排序的部分中不断选最小的,放在已排序部分的后面。
复杂度表现稳定,但是不稳定排序。
插入排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 |
假设前 $i$ 个数已经有序,取第 $i+1$ 个数,然后向前扫描,直到某个数 $a_j\le a_{i+1}$ ,将 $a_{i+1}$ 插入到 $a_j$ 后面。初始 $i=1$ 。
希尔排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n^{1.3})$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 不稳定 |
作者: dreamcatcher-cx 出处: https://www.cnblogs.com/chengxiao/ 本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在页面明显位置给出原文链接。
我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,n/2,(n/2)/2,...,1,称为增量序列。
希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
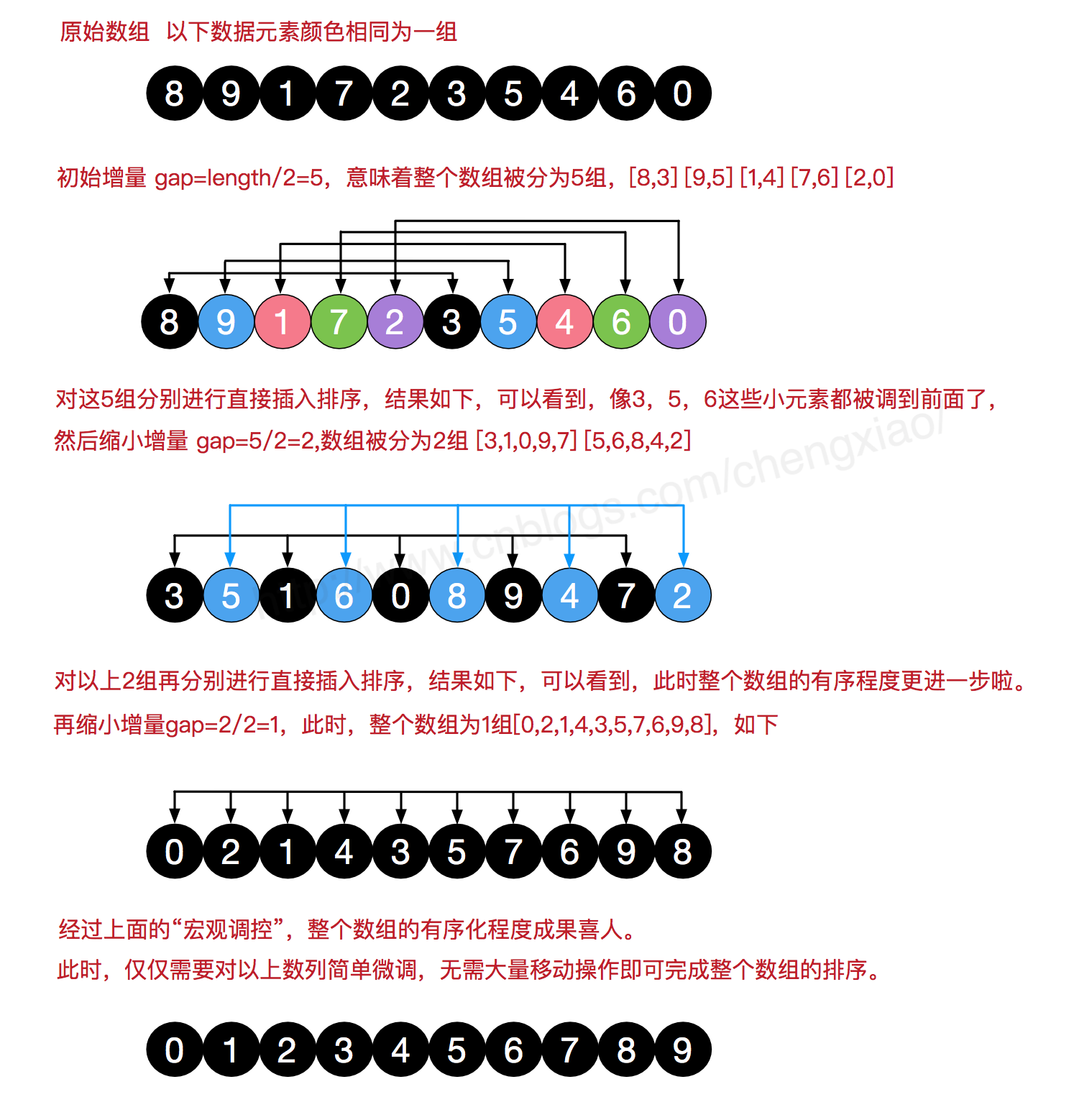
例题:设一组初始记录关键字序列为(50,40,95,20,15,70,60,45),则以增量d=4的一趟希尔排序结束后前4条记录关键字为()。
- A、40,50,20,95
- B、15,40,60,20
- C、15,20,40,45
- D、45,40,15,20
答案:B
桶排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n+k)$ | $O(n^2)$ | $O(n)$ | $O(n+k)$ | 稳定 |
为何最坏为 $O(n^2)$ ?若所有数都一样,当前桶被占用,需要向后寻找直到空桶。
堆排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(1)$ | 不稳定 |
顾名思义,每次用堆得到一个最大/最小值,$n$ 次操作即可得到有序数列。
归并排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(n)$ | 稳定 |
不断将数列二分然后分治,排序后合并。
复杂度表现稳定,也是稳定排序。
快速排序
| 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|
| $O(n\log n)$ | $O(n^2)$ | $O(n\log n)$ | $O(n\log n)$ | 不稳定 |
从数列中选出一个数作为基准,将比基准小的数放在基准前,比它大的放在后,此时基准的顺序一定是正确的。而后对前后两个部分分治。(类似于归并)
std:sort
std::sort 在数据量大时采用快排,分段递归排序;一旦分段后的数据小于某个值,就改用插入排序;如果递归层次过深,还会改用堆排序。std::sort使用了快排,插入排序(希尔排序),堆排序。
例题:c++的std::sort实现中使用了以下哪些快速排序的算法()
- A、快速排序
- B、堆排序
- C、基数排序
- D、插入排序(希尔排序)
答案:ABD
归并排序
运用递归将原数据不断二分,然后在回溯过程中使用归并算法将其一步步合并,最后合成一个有序数列。
时间效率:最好:$ O(log n) $ 最坏:$ O(n \times log n) $
其中归并就是将两个数组一个个比较即可,最多比较 $ 2n-1 $ 次。
例(NOIp2017 T11):设 A 和 B 是两个长为 n 的有序数组,现在需要将 A 和 B 合并成一个排好序的 数组,请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 ( )次比较。
答案:$ 2n-1 $
表达式
中缀表达式
就是一般人用的表达式,初赛肯定不会考。
前缀表达式
以下内容转载至:https://www.cnblogs.com/chensongxian/p/7059802.html
就是把运算符放到数字的前面。
前缀表达式的计算:从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 op 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
中缀转前缀:
- 初始化两个栈:运算符栈s1,储存中间结果的栈s2
- 从右至左扫描中缀表达式
- 遇到操作数时,将其压入s2
遇到运算符时,比较其与s1栈顶运算符的优先级
- 如果s1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈
- 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入s1
- 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较
遇到括号时
- 如果是右括号“)”,则直接压入s1
- 如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃
- 重复步骤2至5,直到表达式的最左边
- 将s1中剩余的运算符依次弹出并压入s2
- 依次弹出s2中的元素并输出,结果即为中缀表达式对应的前缀表达式
后缀表达式
把运算符放到数字的右边。
后缀表达式的运算:从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 op 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
中缀转前缀:和中缀转后缀差不多,就是从左到右扫,最后逆序就行了。
例(NOIp2017 T7):表达式 a (b + c) d 的后缀形式是( )。
- A. a b c d +
- B. a b c + d
- C. a b c + d
- D. b + c a d
答案:B
图
相关定义
完全图:每对顶点都有边相连的图。
完全无向图有 $ \dfrac {n\times \left( n-1\right) }{2} $ 条边,完全有向图有 $ n\times \left( n-1\right) $条边。
连通图:每两个节点间都有路径相连的图。
例题
例1:(NOIp2017 T8) 由四个不同的点构成的简单无向连通图的个数是( )。
答案:38
解析:按照分类标准连1条、连2条、连3条、连4条、连5条、连6条分类讨论。其中连1条、连2条由于无法构成无向连通图而舍掉。再对剩下的情况进行组合(因为无向),即在6条可能的边中连上3、4、5或6条,并将可以构成无向连通图的情况进行计数。不能构成的情况其实应该只有连3条边时才出现。比如ABCD 4个点三条边分别连接A-B、B-C、C-A就不行,一共四种不行的。算出来一共是42-4=38种。
例2:(NOIp2016 T8) G 是一个非连通简单无向图,共有 28 条边,则该图至少有( )个顶点。
答案:9
解析:因为是非连通图,所以至少有一个点不能连通,那么建一个完全图再把顶点+1即可。
$ \dfrac {n\times \left( n-1\right) }{2} = 28 $ ,解得 $ n=8 $ ,答案为 $ n+1=9 $。
递推时间复杂度的计算——主定理(Master Theorem)
以下内容来自OI Wiki,全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用
我们可以使用 Master Theorem 来快速的求得关于递归算法的复杂度。 假设我们有递推关系式
$$ T(n) = AT\left( \dfrac {n}{b}\right) +cn^{k} \qquad \forall n > b $$
那么
$$ T(n) = \begin{cases}\Theta(n^{\log_b a}) & a > b^k \\ \Theta(n^k) & a< b^k \\ \Theta(n^k\log n ) & a = b^k \end{cases} $$
较复杂的排列组合(见pdf)
例1(2008,22)书架上有21本书,编号从1到21,从其中选4本,其中每两本的编号都不相邻的选法一共有(3060)种。(等价放了17本书,插入4本,$C_{18}^4=3060$)
运算符优先级(部分)
| 优先级 | 运算符 |
|---|---|
| 1 | 后缀++ --,括号 |
| 2 | 前缀++ --,! ~ |
| 3 | * / % |
| 4 | + - |
| 5 | << >> |
| 6 | == != |
| 7 | & |
| 8 | ^ |
| 9 | | |
| 10 | && |
| 11 | || |
例题:(2017,5)在C语言中,表达式 23|2^5 的值是( ) 23
欧拉图
- 定义:通过图中所有边且每边仅通过一次的通路称为欧拉回路,具有欧拉回路的图称为欧拉图。
- 具有欧拉通路而无回路的称为半欧拉图。
- 无向连通图是欧拉图:图中不含奇数度节点
- 无向连通图含欧拉通路:有0个或2个奇数度的节点
- 有向连通图是欧拉图:所有节点入度=出度
- 有向连通图含欧拉通路:所有节点入度=出度 或 除了两个节点(起点终点),其他节点满足入度=出度,且这两点中起点入度=出度-1,终点出度=入度-1。
- 欧拉环游,欧拉闭迹
例题:(2007,9)欧拉图G 是指可以构成一个闭回路的图,且图G 的每一条边恰好在这个闭回路上出现一次(即一笔 画成)。在以下各个描述中,不一定是欧拉图的是(D)。
- A.图G中没有度为奇数的顶点
- B.包含欧拉环游的图(欧拉环游是指通过图中每边恰好一次的闭路径)
- C.包含欧拉闭迹的图(欧拉迹是指通过图中每边恰好一次的路径)
- D.存在一条回路,通过每个顶点恰好一次
- E.本身为闭迹的图
数学中逻辑符号
¬=!∧=&∨=|
例1:(2007,11)设A=B=true,C=D=false,以下逻辑运算表达式值为真的有(ABC)。
- A. (¬ A∧B)∨(C∧D∨A)
- B. ¬ (((A∧B)∨C)∧D)
- C. A∧(B∨C∨D)∨D
- D. (A∧(D∨C)) ∧B
例2:(2008,13)设A=true,B=false,C=true,D=false,以下逻辑运算表达式值为真的有(AC)。
- A. (A∧B)∨(C∧D∨A)
- B. ((A∧B)∨C)∧D
- C. (B∨C∨D)∨D∧A
- D. A∧(D∨C)∧B
字符串
- 子串:串中任意个连续的字符组成的子序列称为该串的子串。
- $n$ 个字符的串的子串个数:$\frac{n(n+1)}{2}+1$ (注意空串)
例题:(2008,3)设字符串S=”Olympic”,S的非空子串的数目是(28)。
补充:哈夫曼编码
将字符按照出现的频率建立哈夫曼树,从根节点开始,左子树为0,右子树为1,走到该字符得到该字符的编码。
例题:(2009,7)最优前缀编码,也称Huffman编码。这种编码组合的特点是对于较频繁使用的元素给与较短的唯一编码,以提高通讯的效率。下面编码组合哪一组不是合法的前缀编码。(B)
- A.(00,01,10,11)
- B.(0,1,00,11)
- C.(0,10,110,111)
- D.(1,01,000,001)
立体几何
例题:(2010,18)一个平面的法线是指与该平面垂直的直线。过点(1,1,1)、(0,3,0)、(2,0,0)的平面的法线是(D)。(3,2,1)
- A.过点(1,1,1)、(2,3,3)的直线
- B.过点(1,1,1)、(3,2,1)的直线
- C.过点(0,3,0)、(-3,1,1)的直线
- D.过点(2,0,0)、(5,2,1)的直线
其他题选讲
- (2008,10)对有序数组{5, 13, 19, 21, 37, 56, 64, 75, 88, 92, 100}进行二分查找,等概率的情况下查找成功的平均查找长度(平均比较次数)是(3)。(56查1次,19和88查2次,剩下的数4个查3次,4个查4次(写法不同))
- (2010,17)关于拓扑排序,下列说法正确的是(D)。
- A.所有连通的有向图都可以实现拓扑排序
- B.对同一个图而言,拓扑排序的结构是唯一的
- C.拓扑排序中入度为0的结点总会排在入度大于0的结点的前面
- D.拓扑排序结果序列中的第一个结点一定是入度等于0的点