A.SwapSort
题意
题解
先离散化,然后第 $i$ 位把 $i$ 换过来就行了。
#include<bits/stdc++.h>
#define mp make_pair
#define pii pair<int,int>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=3005;
pii ans[N];
int n,acnt,a[N],b[N],rk[N];
inline bool cmp(int x,int y) { return a[x]<a[y]; }
signed main()
{
n=read();
for (int i=1;i<=n;i++) a[i]=read(),b[i]=i;
sort(b+1,b+n+1,cmp);
for (int i=1;i<=n;i++) rk[b[i]]=i;
for (int i=1;i<=n;i++)
{
if (rk[i]==i) continue;
int j=1;
for (;j<=n && rk[j]!=i;j++);
swap(rk[i],rk[j]);
ans[++acnt]=mp(i-1,j-1);
}
printf("%d\n",acnt);
for (int i=1;i<=acnt;i++) printf("%d %d\n",ans[i].first,ans[i].second);
return 0;
}BerSU Ball
题意
题解
二分图匹配裸题。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=105;
struct Edge {
int next,to;
} edge[N*N];
bool vis[N];
int cnt,head[N],n,m,ans,a[N],b[N],mch[N];
inline void add(int u,int v)
{
edge[++cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt;
}
bool find(int x)
{
for (int i=head[x];i;i=edge[i].next)
{
int y=edge[i].to;
if (vis[y]) continue;
vis[y]=1;
if (!mch[y] || find(mch[y])) return mch[y]=x,1;
}
return 0;
}
signed main()
{
n=read();
for (int i=1;i<=n;i++) a[i]=read();
m=read();
for (int i=1;i<=m;i++) b[i]=read();
for (int i=1;i<=n;i++)
{
for (int j=1;j<=m;j++)
{
if (abs(a[i]-b[j])>1) continue;
add(i,j);
}
}
for (int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
ans+=find(i);
}
return !printf("%d",ans);
}C.Given Length and Sum of Digits...
题意
题解
贪心水题。注意判断无解以及首位不为 $0$ 。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
int n,s;
signed main()
{
n=read(); s=read();
if ((!s && n>1) || s>n*9) return 0&puts("-1 -1");
if (!s && n==1) return 0&puts("0 0");
for (int i=1,j=0;i<=n;i++)
{
int mn=s-(n-i)*9-j,cur=max(i==1 ? 1 : 0,mn);
printf("%d",cur);
j+=cur;
}
printf(" ");
for (int i=1,j=0;i<=n;i++)
{
int mx=s-j,cur=min(9,mx);
printf("%d",cur);
j+=cur;
}
return 0;
}D.Unbearable Controversy of Being
题意
给出一个 $n(\le 3000)$ 点 $m(\le 30000)$ 边的有向图,求形如
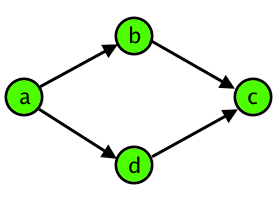
的图形个数
题解
枚举点 $a$ ,对所有拓展两层后到达的点 $c$ 记录到达次数 $in[c]$ ,点 $i$ 对答案的贡献即为 $\frac{in[c]\times (in[c]-1)}{2}$
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
char ch=getchar(); ll f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const ll N=3005;
struct Edge {
ll next,to;
} edge[N*10];
ll n,m,a,b,cnt,ans,head[N],in[N];
inline void add(ll u,ll v)
{
edge[++cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt;
}
inline void work(ll s)
{
queue <ll> q;
memset(in,0,sizeof(in));
for (ll i=head[s];i;i=edge[i].next) q.push(edge[i].to);
while (!q.empty())
{
ll x=q.front(); q.pop();
for (ll i=head[x];i;i=edge[i].next)
{
ll y=edge[i].to;
if (y==s) continue;
in[y]++;
}
}
for (ll i=1;i<=n;i++) ans+=in[i]*(in[i]-1)/2;
}
signed main()
{
n=read(); m=read();
for (ll i=1;i<=m;i++)
{
a=read(); b=read();
add(a,b);
}
for (ll i=1;i<=n;i++) work(i);
return !printf("%lld",ans);
}E.Hiking
题意
有 $n(\le 1000)$ 个点,每个点在 $x_i$ ,权值为 $b_i$ 。一个人从 $0$ 出发到第 $n$ 个点,每天选择一个点停留。他计划每天走 $l$ 的路,如果实际走了 $s$ ,那么会产生 $\sqrt{|s-l|}$ 的不愉快值。求
$$\dfrac{\sum (s_i-l)}{\sum b_i}$$
的最小值。
题解
$0/1$ 分数规划。令原式 $=ans$ ,即
$$\sum (s_i-l) = ans\times \sum b_i \tag{1}$$
$$\sum (s_i-l) - ans\times \sum b_i = 0 \tag{2}$$
要使得 $ans$ 尽可能小,$(2)$ 式应 $\geq 0$ 。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=1005;
double f[N];
int n,m,acnt,x[N],b[N],last[N],ans[N];
inline bool check(double mid)
{
for (int i=1;i<=n;i++)
{
f[i]=1e9;
for (int j=i-1;~j;j--)
{
double cur=1.0*sqrt(1.0*abs(m-x[i]+x[j]))-mid*b[i]+f[j];
if (cur<f[i]) f[i]=cur,last[i]=j;
}
}
return f[n]<0;
}
signed main()
{
n=read(); m=read();
for (int i=1;i<=n;i++) x[i]=read(),b[i]=read();
double l=0,r=1e10;
for (int i=1;i<=100;i++)
{
double mid=(l+r)/2;
if (check(mid)) r=mid;
else l=mid;
}
for (int i=n;i;i=last[i]) ans[++acnt]=i;
for (int i=acnt;i;i--) printf("%d ",ans[i]);
return 0;
}F.Special Matrices
题意
有一个 $n\times n(\le 500)$ 的 $0/1$ 矩阵,给出前 $m$ 行。要求每行每列都有两个 $1$ ,求方案数。
题解
用 $f[i][j][k]$ 表示当前第 $i$ 行,还可以放 $1$ 个 $1$ 的列有 $j$ 个,可以放 $2$ 个的列有 $k$ 个。转移方程式为:
$$f[i][j][k]\rightarrow \begin{cases} f[i+1][j+2][k-2] \\ f[i+1][j-2][k] \\ f[i+1][j][k-1] \end{cases}$$
决策分别为 全放在能放 $2$ 个的列、全放能放 $1$ 个的列、两种各放一个。
如果直接开这样的数组空间会炸,不过我们只关心上一层的值,所以只需要开 $2$ 层的数组,每次切换状态并清空即可。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=505;
char s[N];
int n,m,ha,cnt[N],f[2][N][N];
signed main()
{
n=read(); m=read(); ha=read();
for (int i=1;i<=m;i++)
{
scanf("%s",s+1);
for (int j=1;j<=n;j++) cnt[j]+=s[j]=='1';
}
int a=0,b=0;
for (int i=1;i<=n;i++)
{
if (cnt[i]>2) return 0&puts("0");
a+=cnt[i]==1; //初始能放一个的列数
b+=!cnt[i];
}
f[0][a][b]=1; int cur=0;
for (int i=m+1;i<=n;i++)
{
memset(f[cur^=1],0,sizeof(f[cur]));
for (int j=0;j<=n;j++)
{
for (int k=0;k<=n;k++)
{
int &last=f[cur^1][j][k];
if (!last) continue;
if (j && k) f[cur][j][k-1]=(f[cur][j][k-1]+1ll*j*k%ha*last%ha)%ha;
if (j>=2) f[cur][j-2][k]=(f[cur][j-2][k]+1ll*j*(j-1)/2%ha*last%ha)%ha;
if (k>=2) f[cur][j+2][k-2]=(f[cur][j+2][k-2]+1ll*k*(k-1)/2%ha*last%ha)%ha;
}
}
}
return !printf("%d",f[cur][0][0]);
}