赛前,ljq:不得了,6个人开黑,上紫稳了啊。
10+min过去,大家都A了2道,ljq:这场怕不是要AK。
最后
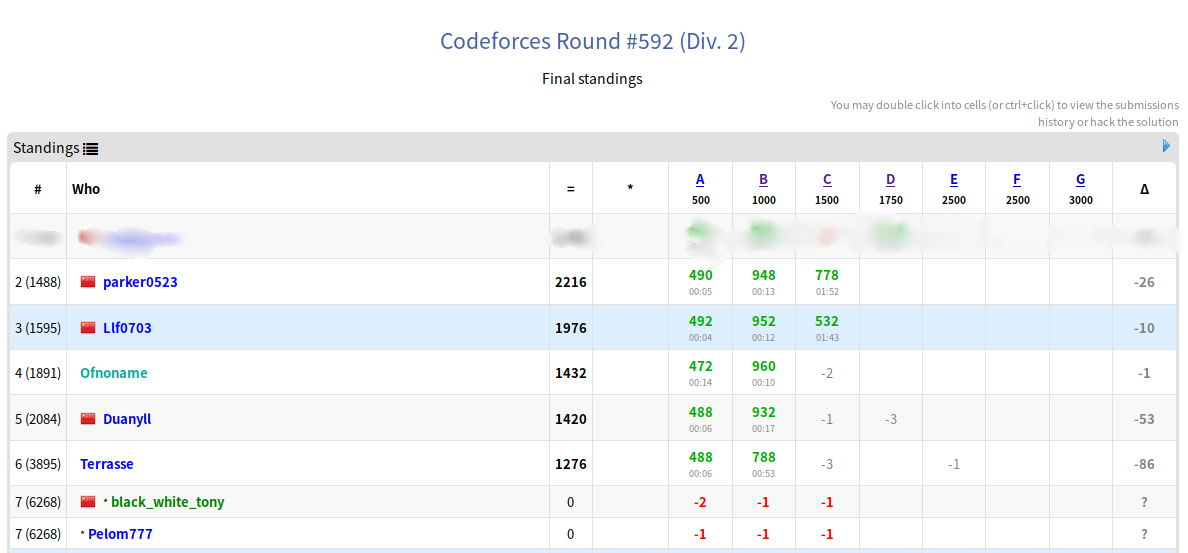
辣鸡C题,毁我青春。
不过还是得怪做题策略有问题,如果直接跳过C去做DE应该都能A掉,这次就算是用rating买教训了。
A.Pens and Pencils
过水已略
B.Rooms and Staircases
题意
我相信过不了多久洛谷上就会有翻译了
题解
可以发现答案一定是从某一端出发,到达最远的梯子,然后到另一端并返回。我代码还写复杂了点。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
int t,n;
char s[1005];
signed main()
{
t=read();
while (t--)
{
n=read();
scanf("%s",s+1);
int ans=n,i=n;
for (;i && s[i]=='0';i--);
if (!i) { printf("%d\n",ans); continue; } //没梯子
ans=max(ans,i+max(n-i+1,i)); //从左出发
for (i=1;i<=n && s[i]=='0';i++);
ans=max(ans,(n-i+1)+max(n-i+1,i)); //右
printf("%d\n",ans);
}
return 0;
}C.The Football Season
题意
求解方程
$$w\times x+d\times y=p$$
要求 $x+y\le n$ 。
$1\le n\le 10^{12},0\le p\le 10^{17},1\le d < w\le 10^5$ 。
题解
我:C题题意是啥?
ljq:就是解那个方程的非负整数解,exgcd裸题
然后我就敲了exgcd,因为 $w > d$ ,所以让 $y$ 尽可能小肯定最优。
WA了。后来发现 $p\le 10^{17}$ ,直接 $\times \frac{p}{\gcd (w,d)}$ 显然会爆。
那总不可能写高精吧,去看status发现无数老哥交 Pypy3 ,于是我就开始改python,中途因为 //= 写成 /= 等原因一共WA了7发,最后A的时候就只剩500多分了。另外3个人去改我的变量名分都比我高虽然有两个被skip掉了
n,p,w,d=[int(i) for i in input().split(" ")]
def exgcd(a,b):
if b==0:
return (1,0)
tx,ty=exgcd(b,a%b)
return (ty,tx-a//b*ty)
def gcd(a,b):
if b==0:
return a
return gcd(b,a%b)
x,y=exgcd(w,d)
g=gcd(w,d)
if p%g!=0:
print("-1")
exit()
p//=g
x*=p
y*=p
w//=g
d//=g
if x<0: #把 x 变成非负
tmp=(-x+d-1)//d
x+=tmp*d
y-=tmp*w
if y<0: #把 y 变成非负
tmp=(-y+w-1)//w;
y+=tmp*w
x-=tmp*d
if x<0:
print("-1")
exit()
if y>=w: #让 y 尽可能小
tmp=y//w
y-=tmp*w;
x+=tmp*d;
if x+y>n:
print("-1")
exit()
print(int(x),int(y),int(n-x-y))赛后看其他人的写法,发现其实并不需要用 exgcd 来解方程。$y$ 的最小值就是 $\dfrac{p}{d}\mod w$ ,然后 $x=\dfrac{p-d\times y}{w}$ 。
不过还是需要 exgcd 来求个逆元。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
char ch=getchar(); ll f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
ll n,p,w,d;
ll gcd(ll x,ll y) { return y ? gcd(y,x%y) : x; }
ll exgcd(ll l,ll r,ll &x,ll &y)
{
if (!r)
{
x=1; y=0;
return l;
}
ll ans=exgcd(r,l%r,y,x);
y-=l/r*x;
return ans;
}
inline ll inv(ll a,ll ha)
{
ll x=0,y=0;
exgcd(a,ha,x,y);
return (x+ha)%ha;
}
signed main()
{
n=read(); p=read(); w=read(); d=read();
ll g=gcd(w,d);
if (p%g) return 0&puts("-1"); //无解
p/=g; w/=g; d/=g; //除了gcd方程等价
ll y=p%w*inv(d,w)%w,x=(p-y*d)/w; //直接算出 x,y
if (x<0 || x+y>n) return 0&puts("-1"); //无解
return !printf("%lld %lld %lld",x,y,n-x-y);
}D.Paint the Tree
题意
用 $3$ 种颜色给一棵 $n(\le 10^5)$ 个点的树染色,每个点染不同的颜色有不同的代价。要求由任意 $3$ 个点组成的链上颜色都不相同,求代价的最小值。
题解
可以发现如果不是链就无解。
证明:从树的直径出发,如果染了前两个点,那么直径上后面的颜色都是确定的。如果不是链的话那一定会有分叉,假设形如下图,其中 a--b--c 是直径:
a--b--c
|
da 和 c 的颜色一定不同,所以 d 不管染什么颜色都不满足题解。
所以就枚举前两个点的颜色,依次遍历链上每一个点即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=100005;
struct Edge {
int next,to;
} edge[N<<1];
vector <int> v;
ll ans=1e18;
int n,a,b,cnt,head[N],c[4][N],deg[N],colRes[N],colAns[N];
inline void add(int u,int v)
{
edge[++cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt;
}
signed main()
{
n=read();
for (int i=1;i<=3;i++) for (int j=1;j<=n;j++) c[i][j]=read();
for (int i=1;i<n;i++)
{
a=read(); b=read();
add(a,b); add(b,a);
deg[a]++; deg[b]++;
}
for (int i=1;i<=n;i++) if (deg[i]==1) v.push_back(i);
if (v.size()!=2) return 0&puts("-1"); //不是链则无解
int x=v[0],y; //链上的一端
y=edge[head[x]].to; //第二个点
for (int j=1;j<=3;j++) //第一个点染的颜色
{
for (int k=1;k<=3;k++) //第二个点的颜色
{
if (j==k) continue;
colRes[x]=j; colRes[y]=k;
ll res=c[j][x]+c[k][y]; //当前答案
int cur=y,fa=x,last1=j,last2=k; //当前点,父节点,前两个点的颜色
for (int i=3;i<=n;i++)
{
int nxt;
for (int p=head[cur];p;p=edge[p].next) if ((nxt=edge[p].to)!=fa) break; //nxt 是下一个点
fa=cur; cur=nxt;
int col=1; for (;col==last1 || col==last2;col++); //找到符合要求的颜色
res+=c[col][cur];
colRes[cur]=col;
last1=last2; last2=col;
}
if (res<ans) //更新答案
{
ans=res;
memcpy(colAns,colRes,sizeof(colRes));
}
}
}
printf("%lld\n",ans);
for (int i=1;i<=n;i++) printf("%d ",colAns[i]);
return 0;
}E.Minimizing Difference
题意
给出 $n(\le 10^5)$ 个数,可以进行 $k$ 次操作,每次可以把一个数 $+1$ 或 $-1$ 。求操作后 最大数和最小数差值 的最小值。
题解
可以发现最优的操作就是把两端的最值不断往中间靠近。而最值的点可能有多个,假设有 $x$ 个,那么每消耗 $x$ 才能使答案 $-1$ ,所以每次都选择个数较少的一端进行操作。
需要离散化得到各个数值的个数。因为我比较懒所以操作的过程就写的优先队列。
#include<bits/stdc++.h>
#define mp make_pair
#define pii pair<ll,ll>
#define pip pair<ll,pii>
#define ll long long
using namespace std;
inline ll read()
{
char ch=getchar(); ll f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const ll N=100005;
struct node {
ll s,cnt;
} s[100005];
ll n,m,k,ans=1e9,a[100005];
priority_queue <pip,vector<pip>,greater<pip> > q;
signed main()
{
n=read(); k=read();
for (ll i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
for (ll i=1;i<=n;i++) //离散化
{
if (a[i]!=a[i-1]) s[++m].s=a[i],s[m].cnt=1;
else s[m].cnt++;
}
if (m==1) return 0&puts("0"); //只有一个值
q.push(mp(s[1].cnt,mp(1,0))); //左端
q.push(mp(s[m].cnt,mp(m,1))); //右端
for (ll l=1,r=m;!q.empty();q.pop())
{
ll x=q.top().second.first,y=q.top().first;
bool p=q.top().second.second; //在哪一端
ll delta=p ? s[x].s-s[x-1].s : s[x+1].s-s[x].s; //差值
if (delta*y<=k) //如果能直接靠近到下一个数值
{
k-=delta*y;
if (p) //在右端
{
r--;
q.push(mp(y+s[r].cnt,mp(r,1)));
}
else
{
l++;
q.push(mp(y+s[l].cnt,mp(l,0)));
}
if (l==r) { ans=0; break; }
}
else //否则能靠近多少算多少
{
ll maxd=k/y; //最多能靠近的值
ans=s[r].s-s[l].s-maxd;
break;
}
}
return !printf("%lld",ans);
}F.Chips
题意
题解
看题解看到的神仙做法。
有两个结论:
- 当前回合没被修改的点,设为 $x$ ,以后都不会被修改
- 与 $x$ 相邻的点在下一回合也不会修改
第 $1$ 个结论比较显然。对于第 $2$ 个结论,因为 $x$ 没变,所以它左右两个也不会变。
开个队列,把不需要修改的节点不断入队,并标记它第一次没被修改的操作为 $vis[x]$ 。最后通过 $vis[x]$ 的奇偶性即可判断答案。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=200005;
queue <int> q;
char s[N],f[N];
int n,k,vis[N];
signed main()
{
f[0]='B'; f[1]='W';
n=read(); k=read();
scanf("%s",s+1);
for (int i=1;i<=n;i++) s[i]=s[i]=='B' ? 0 : 1; //转为 0/1 序列
for (int i=1;i<=n;i++)
{
int l=i==1 ? n : i-1;
int r=i==n ? 1 : i+1;
if (s[i]==s[l] || s[i]==s[r]) vis[i]=1,q.push(i); //最初不用修改的点
}
while (!q.empty())
{
int x=q.front(); q.pop();
if (vis[x]==k) break;
int l=x==1 ? n : x-1;
int r=x==n ? 1 : x+1;
if (!vis[l]) vis[l]=vis[x]+1,q.push(l);
if (!vis[r]) vis[r]=vis[x]+1,q.push(r);
}
for (int i=1;i<=n;i++)
{
if (!vis[i]) printf("%c",f[s[i]^(k&1)]); //一直被修改,以 k 的奇偶性判断
else printf("%c",f[s[i]^((vis[i]-1)&1)]); //vis[i]-1 是被修改的次数
}
return 0;
}G.Running in Pairs
逆序开题或成最大赢家。 ——洛谷某大佬(忘了是谁了)
为什么要把这题放G啊!
题意
数列 $a={1,2,3,...,n}$ ,求一个 $1..n$ 的排列 $b$ ,使得 $\sum_{i=1}^n \max (a_i,b_i)$ 最大,且 $\le k$ 。
题解
令 $sum=\dfrac{n\times (n+1)}{2}$ ,显然无解的情况就是 $k < sum$ 。
然后依次遍历每一位 $i$,设没有用过的数的区间为 $[L,R]$ 。如果 $sum+R-i\le k$ ,那么就填 $R$ ,否则填 $L$ 。
这个构造的正确性比较显然。当前数填 $R$ 肯定比之后的数填贡献大,所以合法的话就尽量填 $R$ ;如果没法填 $R$ ,那么填其它的 $> L$ 的数也不比后面填优。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
char ch=getchar(); ll f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
ll k,sum;
int n,ans[1000005];
signed main()
{
n=read(); k=read();
if (k<(sum=1ll*(n+1)*n/2)) return 0&puts("-1");
for (int i=1,l=1,r=n;i<=n;i++)
{
if (r<=i) { ans[i]=r--; continue; } //r<=i ,随便填
if (sum+r-i<=k) sum+=r-i,ans[i]=r--;
else ans[i]=l++;
}
printf("%lld\n",sum);
for (int i=1;i<=n;i++) printf("%d ",i);
puts("");
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
return 0;
}
然后机皇 llf 虐场了(
要不是括号没删我就删评了