A.Keanu Reeves
题意
题解
显然答案最多为 $2$ 。如果本来就不一样多,答案就是 $1$ ;否则把第一个数划出去即可,答案为 $2$ 。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
int n;
char s[105];
signed main()
{
n=read();
scanf("%s",s+1);
int sum=0;
for (int i=1;i<=n;i++) sum+=s[i]-'0';
if (sum*2!=n) return !printf("1\n%s",s+1);
return !printf("2\n%c %s",s[1],s+2);
}B.Number Circle
题意
题解
先从大到小排序,可以发现如果 $a_1 \geq a_2+a_3$ 就无解,否则都可以构造出解。
构造的方法为把 $a_1$ 放在中间,然后把次小的两个放在两边,再在两边放更次小的……,构成一个如下的序列:
$$...,a_5,a_3,a_1,a_2,a_4,a_6,...$$
这样可以保证每个数的旁边都有个比它大的,一定满足条件。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=300005;
int n,l,r,s[N],ans[N];
signed main()
{
n=read();
for (int i=1;i<=n;i++) s[i]=read();
sort(s+1,s+n+1,[](int x,int y){ return x>y; });
if (s[1]>=s[2]+s[3]) return 0&puts("NO");
puts("YES");
ans[l=r=(n+1)>>1]=s[1];
for (int i=2;i<=n;i++)
{
if (i&1) ans[--l]=s[i];
else ans[++r]=s[i];
}
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
return 0;
}C.Candies!
题意
题解
比较显然的倍增题,题中的操作就是倍增的过程。
用 $sum[i][j]$ 表示从 $i$ 开始往后 $2^j$ 个数的和,$f[i][j]$ 表示答案。如果 $sum[i][j] > 10$ ,那么对答案 $f[i][j]$ 有 $1$ 的贡献。最后 $sum[i][j]$ 要 $\mod 10$ 。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=100005;
int n,m,a,b,f[N][18],s[N][18];
signed main()
{
n=read();
for (int i=1;i<=n;i++) s[i][0]=read();
for (int j=1;j<=17;j++)
{
int maxi=n-(1<<j)+1;
for (int i=1;i<=maxi;i++)
{
s[i][j]=s[i][j-1]+s[i+(1<<(j-1))][j-1];
f[i][j]=f[i][j-1]+f[i+(1<<(j-1))][j-1];
if (s[i][j]>=10) s[i][j]-=10,f[i][j]++;
}
}
m=read();
while (m--)
{
a=read(); b=read();
b-=a-1; //区间长度
int j=0;
for (int i=1;i<b;i<<=1,j++); //确定 j
printf("%d\n",f[a][j]);
}
return 0;
}D1.Add on a Tree
题意
题解
可以发现如果存在两条边是“绑定”在一起的,即修改其中一条边必定同时修改另一条边,那么无解,因为这两条边的权值不可能不同。
如果存在一个点度数为 $2$ ,那么与它相连的两条边就是“绑定”在一起的,因为一条边被修改后,除了另一条边外没有别的路径,此时无解。
其它情况都是可以构造出解的,详见下面的 D2 。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
int n,a,b,deg[100005];
signed main()
{
n=read();
for (int i=1;i<n;i++)
{
a=read(); b=read();
deg[a]++; deg[b]++;
}
for (int i=1;i<=n;i++) if (deg[i]==2) return 0&puts("NO");
return 0&puts("YES");
}D2.Add on a Tree: Revolution
题意
题解
跟上一题一样,存在度数为 $2$ 的点就无解。
要修改边 $(u,v)$ 的边权为 $x$,可以找出与 $u$ 相连的两个叶子 $(u_1,u_2)$ ,特殊的,如果 $u$ 就是叶子,那么 $u_1=u_2=u$ 。同理找出 $(v_1,v_2)$ 。
用 $(u,v,w)$ 表示给路径 $u\rightarrow v$ 加上权值 $w$ ,则操作如下:
$(u_1,v_1,\frac{x}{2})$ , $(u_2,v_2,\frac{x}{2})$ , $(u_1,u_2,-\frac{x}{2})$ , $(v_1,v_2,-\frac{x}{2})$
如下图所示:
图片来自 https://blog.csdn.net/m0_37809890/article/details/95385922 ,遵循 CC 4.0 BY-SA 版权协议
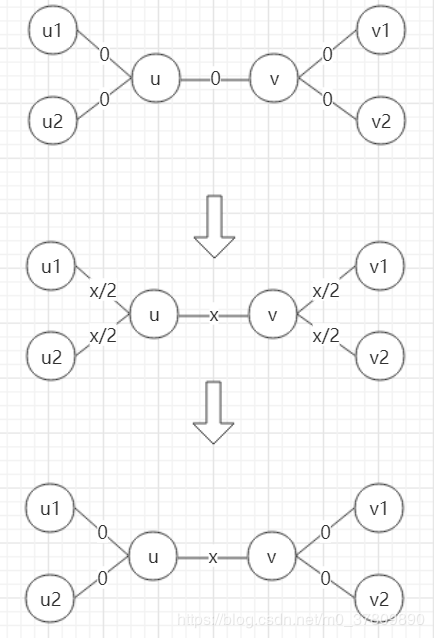
遍历每一条边,对边的两个端点搜索出 $u_1,u_2,v_1,v_2$ ,然后按照上述方法操作即可。复杂度 $O(n^2)$ 。
#include<bits/stdc++.h>
#define mp make_pair
#define pii pair<int,int>
using namespace std;
inline int read()
{
char ch=getchar(); int f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
const int N=100005;
struct Edge {
int next,from,to,w;
} edge[N<<1];
struct out {
int u,v,w;
} res[N<<2];
int n,a,b,c,cnt,ans,rcnt,head[N],deg[N];
inline void add(int u,int v,int w)
{
edge[++cnt].to=v;
edge[cnt].w=w;
edge[cnt].from=u;
edge[cnt].next=head[u];
head[u]=cnt;
}
int dfs(int x,int f) //从 x 出发找叶子节点
{
if (deg[x]==1) return x;
for (int i=head[x];i;i=edge[i].next)
{
int y=edge[i].to;
if (y==f) continue;
return dfs(y,x);
}
return 0;
}
inline pii find(int x,int f) //找到 u1,u2
{
if (deg[x]==1) return mp(x,x); //叶子节点,u1=u2=u
int a=0,b=0;
for (int i=head[x];i;i=edge[i].next)
{
int y=edge[i].to;
if (y==f) continue;
int res=dfs(y,x);
if (!a) a=res;
else if (!b) { b=res; break; }
}
return mp(a,b);
}
signed main()
{
n=read();
for (int i=1;i<n;i++)
{
a=read(); b=read(); c=read();
add(a,b,c); add(b,a,c);
deg[a]++; deg[b]++;
}
for (int i=1;i<=n;i++) if (deg[i]==2) return 0&puts("NO");
for (int i=1;i<=cnt;i+=2)
{
int u=edge[i].from,v=edge[i].to,w=edge[i].w;
pii ux=find(u,v),vx=find(v,u);
int u1=ux.first,u2=ux.second,v1=vx.first,v2=vx.second;
if (u1!=v1) res[++rcnt]=(out){u1,v1,w>>1};
if (u2!=v2) res[++rcnt]=(out){u2,v2,w>>1};
if (u1!=u2) res[++rcnt]=(out){u1,u2,-w>>1};
if (v1!=v2) res[++rcnt]=(out){v1,v2,-w>>1};
}
printf("YES\n%d\n",rcnt);
for (int i=1;i<=rcnt;i++) printf("%d %d %d\n",res[i].u,res[i].v,res[i].w);
return 0;
}E.Count Pairs
题意
题解
左右两边同乘 $(a_i-a_j)$ :
$$(a_i+a_j)\times (a_i-a_j)\times ({a_i}^2+{a_j}^2)\equiv k\times (a_i-a_j)\pmod p$$
$$({a_i}^2-{a_j}^2)\times ({a_i}^2+{a_j}^2)\equiv k\times (a_i-a_j)\pmod p$$
$${a_i}^4-{a_j}^4\equiv k\times a_i-k\times a_j\pmod p$$
$${a_i}^4-k\times a_i\equiv {a_j}^4-k\times a_j\pmod p$$
那么对于 $a_i$ ,算出 $({a_i}^4-k\times a_i)\mod p$ ,再用 map 记录这个值有多少个即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
char ch=getchar(); ll f=1,x=0;
while (ch<'0' || ch>'9') { if (ch=='-') f=-1; ch=getchar(); }
while (ch>='0' && ch<='9') { x=x*10+ch-'0'; ch=getchar(); }
return f*x;
}
ll n,p,k,a,ans;
map <ll,ll> mp;
signed main()
{
n=read(); p=read(); k=read();
for (ll i=1;i<=n;i++)
{
a=read();
ll cur=(a*a%p*a%p*a%p-k*a%p+p)%p;
if (mp.count(cur)) ans+=mp[cur];
mp[cur]++;
}
return !printf("%lld",ans);
}F.Array Beauty
做完这题感觉收获巨大,专门开了一篇文章写这道题的题解。